先从冲击函数的定义开始:


我们注意到,冲击函数的这些性质,都有一个前提,那就是时间域是从负无穷到正无穷。
再看冲击函数的频谱:

同样,冲激函数频谱等于1,也是以时间域从负无穷到正无穷为前提。
再看正弦函数和余弦函数的频谱:
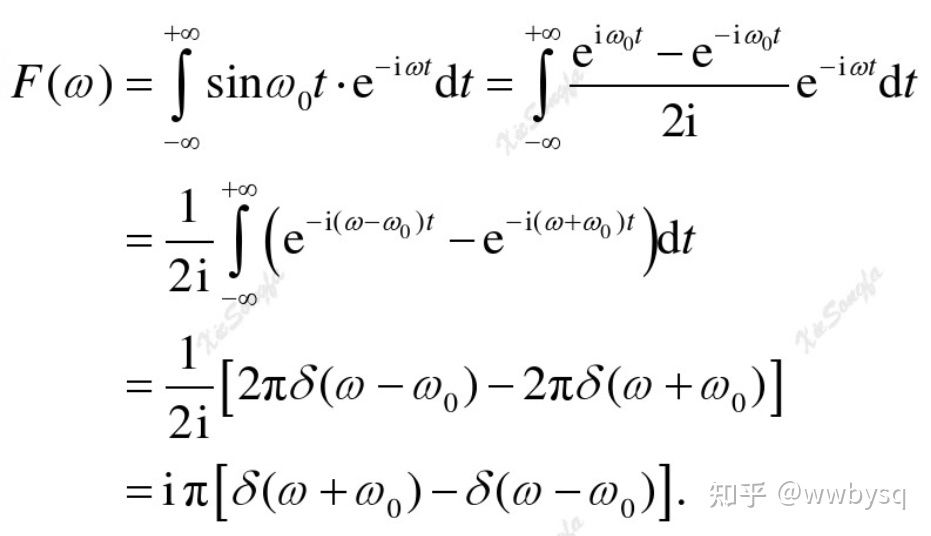
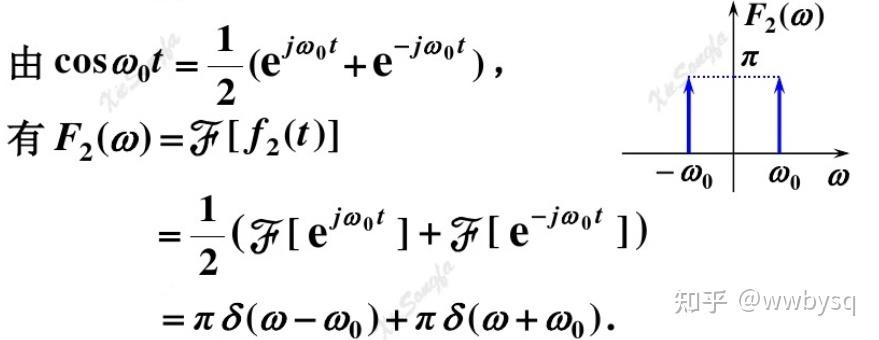
图1
我们看到,正弦余弦函数的频谱,在以整个时间域为前提进行积分以后,他们的频谱都是冲击函数。这也是我们在频谱图上看到一根根竖线的原因,因为按照傅里叶级数分解的原理,函数都可以分解为一个个正弦波之和。
但在实际中进行频谱分析的时候,时间域不可能是无穷大,比如:

在上面无穷长的信号序列里面,截取中间那一部分进行分析,这个时候就会出现所谓的频谱泄露,原因在于积分的时间域变成了有限,假设是【-T,T】,以图1中余弦函数频谱推导中的
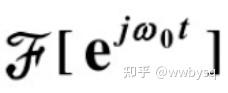
部分进行推导如下:
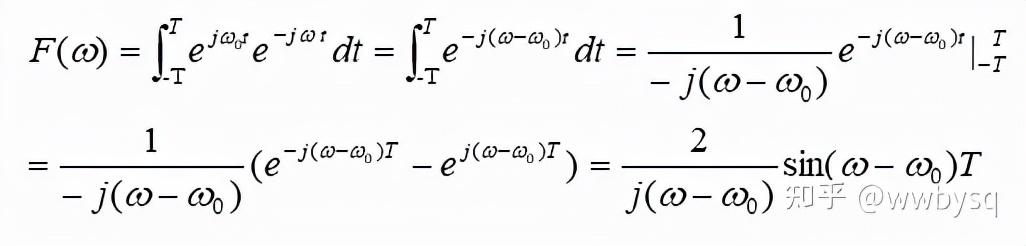
图2
我们看到,其结果其实是一个sinc函数:
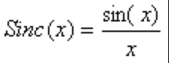
我们知道,当x趋于0时,sinc函数的极限为1,其图像如下:
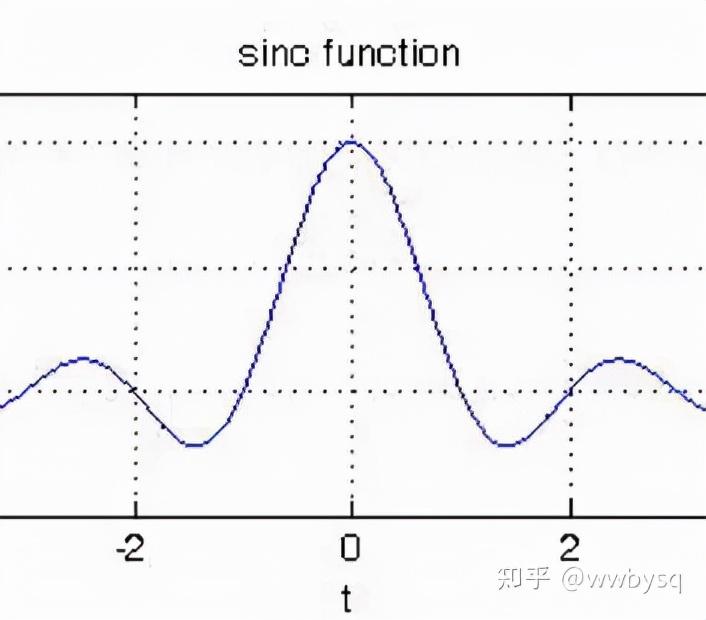
图3
所以,图2中的推导结果表明,w在趋近于w0的时候,其取值最大,但在w0附近的时候,也会逐渐增大,也就是说,本该像图1中的一个冲击序列,变成了图3中的钟形函数,意味着中间频率点w0的信号能量,泄露给了它附近的频率点。
再以一个实例说明:
f(t)=sin(2*pi*t)+0.8*sin(6*pi*t)+0.6*sin(8*pi*t)
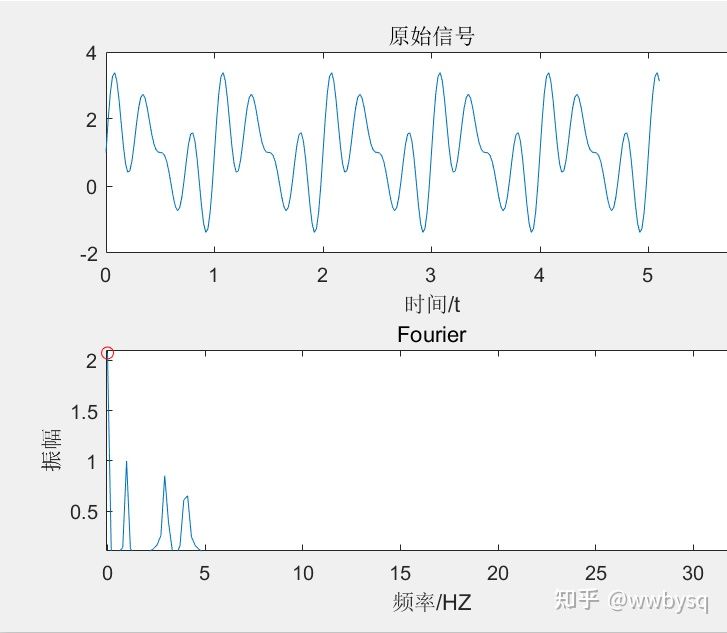
我们看到,每一个正弦波在频谱图中都产生了一根竖线,但在频率点1hz、3hz和4hz附近确实存在着频谱泄露的现象。
总结如下:
1:正弦余弦函数的傅里叶变换结果,表示的是在频谱图上,它们会在自己的频率点上产生一根竖线(冲击序列)。
2:频谱泄露产生的原因在于时间域由理论上的无限变成了实践中的有限。
